I wonder how many concepts from basic mathematics can be applied to things outside of textbooks. I have been enamored by the idea of global maxima and local maxima off late, and I’m trying to incorporate it as best as possible into my professional pursuits.
Often I had been vying for my local maximum’s optimization – getting that title change, getting that raise, working extremely hard – always with respect to nearby peers, as that’s what would constitute my short-sighted local maximum.
It was worthwhile for me every now and then though to zoom out and check out nearby peaks and valleys. Always a good chance that there is a higher peak nearby, which is worth optimizing for more than a current local maximum.
Simply put, working at an acceptable rate in a high return-on-investment game trumps working extremely hard in a low return-on-investment game. Optimizing shit will just give us slightly better shit.
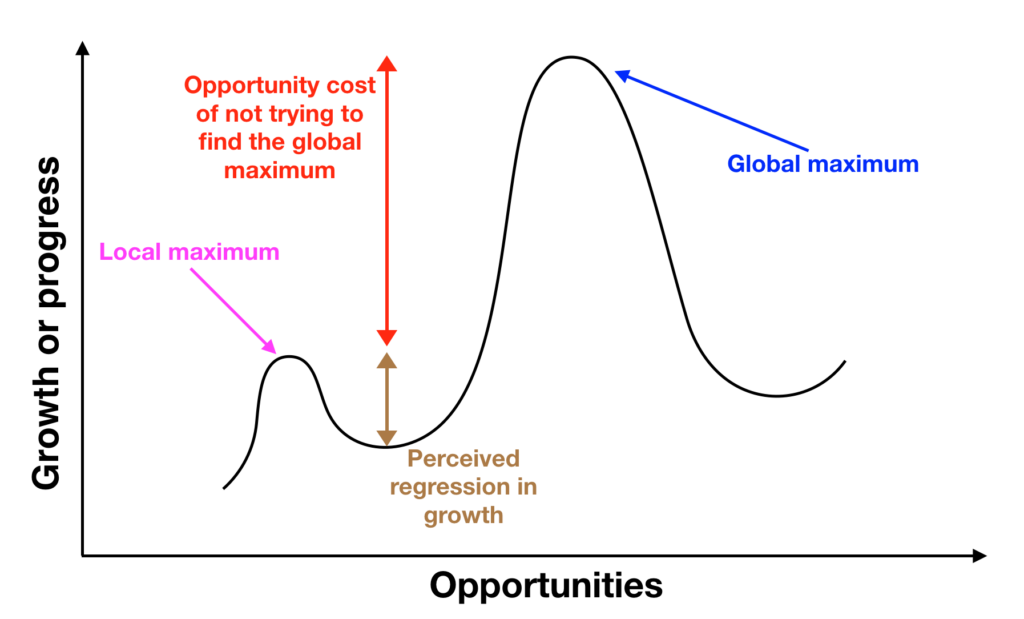
Why should I vie for pennies when something else could afford me opportunities with 1000x impact and wealth generation potential? Being at a 50% achievement level of a super high global maximum may still be better than being at 95% of a lower local maximum. Better to jog slower in the correct / better race, than sprinting in the wrong one.
Easier said than done though, of course, since usually this means that there will be a period of perceived regression in growth during transition periods. And this is often enough to dissuade people from even trying.
In the grand scheme of things however, the opportunity cost of not trying to find the global maximum is usually far greater than the cost of perceived regression in growth.
“Optimizing shit will just give us slightly better shit.” lol. This sentence makes a lot of sense, especially when I relate it with the place I’m currently working in.